Vzhledem ke dvěma parametrům μ, σ představuje výše uvedený předpis nekonečně mnoho podobných funkcí. Naštěstí lze vytvořit normovanou veličinu U = (X – μ)/σ. U je taková jediná náhodná veličina, pro kterou platí EU = 0 a varU = 1 (nemá žádný parametr). Výše uvedený předpis (vzorec) se změní na

Funkce f(u) se nazývá hustota pravděpodobnosti normovaného normálního rozdělení N(0,1). Funkce Φ(t) se nazývá distribuční funkce N(0,1).

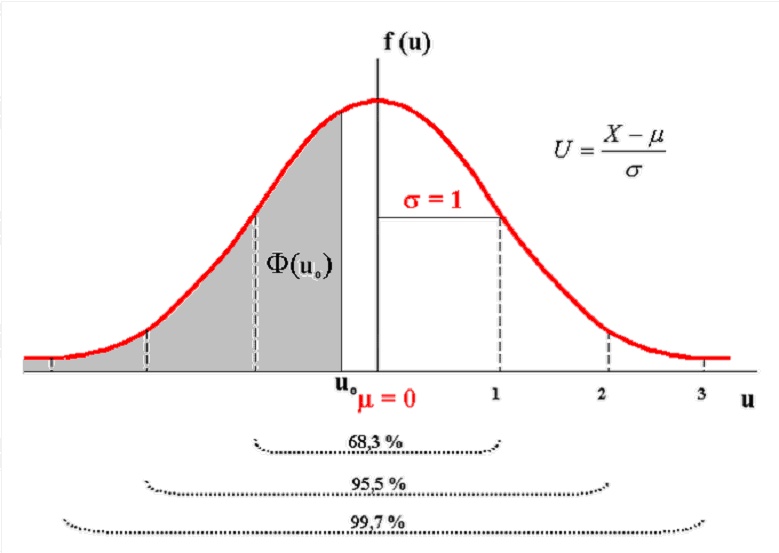
Je zřejmé, že vypočítávat jednotlivé hodnoty distribuční funkce je práce pro počítače. Pro „ruční“ práci se hodí vypracované tabulky. To je právě významná vlastnost distribuční funkce Φ(t) , že je tabelizována. Má tyto další vlastnosti:

Již je to naznačeno na předchozím obrázku, nicméně vyslovme to i slovně. Ať už se zvolí jakékoliv měřítko a ať je rozptyl k průměru v jakémkoliv poměru, normální křivka má vždy některé charakteristické znaky, z nichž uvedeme ty, které jsou pro praxi nejdůležitější. Jestliže pozorujeme plochu ležící pod „zvonem“ jako soubor, leží na obě strany od maxima (střední hodnota, nejčetnější hodnota) vždy přesně stejné části této plochy, a to v úseku mezi +σ a -σ leží 68,26 %, tj. nepatrně více než 2/3 celkové plochy, v úseku mezi +2σ a –2σ skoro přesně 95 % a mezi +3σ a –3σ již 99,7 % plochy.

Pro výpočty potřebujeme ještě použití distribuční funkce Φ(x) pro N(0,1) na případy náhodných veličin X ~ N(μ,σ2). Použije se vzorec:

Pro ilustraci si uvedeme dva jednoduché příklady použití. Hlubší zájemce o toto rozdělení, nechť se podívá do odborných publikací a tabulek.

1. příklad:
Výrobek projde kontrolou, je-li jeho váha v mezích 68-69 g. Plnící stroj je nastaven na μ = 68,3 g a směrodatnou odchylku σ = 0,2 g. Jaká je pravděpodobnost, že náhodně vybraný výrobek kontrolou projde?

Nechť X je náhodná veličina, udávající váhu výrobku v gramech

2. příklad:
Měření vzdáleností mezi dvěma objekty je zatíženo systematickou chybou μ = – 50 cm a náhodnými chybami se směrodatnou odchylkou σ = 100 cm. (Možná jsme hodili do pračky 100 metrové pásmo a ono se srazilo; už měří jen 99,5 metru.) Vypočítejte pravděpodobnost, že chyba jednoho měření nebude větší než 150 cm (-150 < X < +150).